
🚀 博弈论遇上自动驾驶,如何让AI学会“默契”开车?还在为多车交互规划烧脑?德克萨斯大学这篇新论文用“凸集图”把复杂博弈变成了可解的数学题!想第一时间获取这类硬核算法解读、前沿论文速递和行业动态?「龙哥读论文」知识星球每日更新,帮你省下90%的读论文时间!👇扫码加入,解锁自动驾驶、机器人等30+细分领域的前沿干货~

龙哥推荐理由:
这篇论文巧妙地将博弈论与凸优化结合,为多车自动驾驶的“混合整数规划”难题提供了一个优雅且高效的解决方案。它不仅在理论上证明了算法能收敛到安全均衡,仿真结果也展示了其在复杂合并场景下的实用潜力。对于从事自动驾驶规划、多智能体交互的研究者和工程师来说,这是一篇兼具理论深度和工程启发性的佳作。
原论文信息如下:
论文标题:
Game-Theoretic Autonomous Driving: A Graphs of Convex Sets Approach
发表日期:
2026年01月
发表单位:
ETH Zurich; The University of Texas at Austin
原文链接:
https://arxiv.org/pdf/2601.20054v1.pdf
开源代码链接:
https://github.com/TobiaMarcucci/gcsopt
博弈论遇上自动驾驶:多车交互的数学难题
想象一下,你开着车准备并入高速公路。左边有辆车开得很快,你想加速插进去;右边有辆车似乎想让你,但又没完全让。你们彼此猜测着对方的意图,在遵守交通规则的前提下,都想找到对自己最有利的那条路线。这个过程,本质上就是一场博弈。
把场景搬到自动驾驶领域,问题就变成了:如何让一群没有“直觉”和“眼神交流”的AI车辆,安全、高效地完成并线、超车、跟车等操作?传统的规划方法要么把其他车当成不会动的障碍物(太傻),要么假设大家会完全配合(太天真)。现实是,每辆车都有自己的“小算盘”(比如想尽快到达目的地、省油、乘坐舒适),但同时又必须共同遵守“不能撞车”的铁律。图1:高速公路场景下的车辆特定变量(左)和纵向距离示意图(右)。
这就引出了博弈论。用博弈论来建模自动驾驶,就是把每辆车看作一个“玩家”,它们各自优化自己的目标(成本函数),但行动受到其他玩家行动的制约(共享的安全约束)。我们想找到的那个理想状态,叫做广义纳什均衡(Generalized Nash Equilibrium, GNE)。简单说,就是在这个状态下,任何一辆车单方面改变自己的行驶策略(比如突然加速变道),要么会违反安全规则(比如撞车),要么会让自己“更亏”(比如更耗能、更慢)。
听起来很美,但求解GNE是个大难题!因为规划本身是“混合”的:既有离散决策(选哪条车道、什么时候变道),也有连续决策(具体的速度、加速度曲线)。传统的混合整数规划方法在面对多车场景时,计算量会爆炸💥。
德克萨斯大学奥斯汀分校和ETH Zurich的研究者们,祭出了一件“神器”——凸集图(Graphs of Convex Sets, GCS),并提出了一个叫做IBR-GCS的算法,优雅地拆解了这个难题。下面,龙哥就带你盘盘,他们是怎么做到的。凸集图:将混合规划“化整为零”的利器
首先,我们来认识一下今天的主角之一:凸集图。你可以把它想象成一个“乐高”式的规划框架。
顶点(Vertex):每个顶点代表一个“安全的乐高积木块”,它是一个凸集(Convex Set)。在自动驾驶场景里,这个“积木块”可能代表了在某个特定时刻、某条特定车道上,一个安全、无碰撞的纵向位置区间(比如“在前车后方20米到后车前方30米之间的那段路”),以及允许的速度范围。
边(Edge):连接两个顶点的边,代表从上一个时刻的“积木块”转移到下一个时刻的“积木块”是动态可行的。这意味着,车辆可以通过合理的加速度、遵守车道变换规则(比如只能变到相邻车道),安全地从A点开到B点。每条边也有一个成本,比如加速度大小、偏离理想车道的程度等。图2(左):高速公路上的一组车辆,其中红色车辆的安全间隙用绿色标出。图3(右):时间展开图,展示了顶点和边如何连接。
于是,为一辆车做轨迹规划,就变成了在这个庞大的、按时间和车道展开的“乐高建筑图”里,找一条从起点(初始状态)到终点(规划时域末端)的成本最低的路径!
GCS的妙处在于,它把原本纠缠在一起的离散选择(选哪个车道/安全间隙)和连续优化(具体怎么开)给解耦了。离散选择体现在你选哪条“路径”,连续优化则内嵌在每个顶点和边的凸集约束与成本计算中。更重要的是,这个最短路径问题可以被松弛成一个纯粹的凸优化问题来高效求解,并且在很多实际场景下,这个松弛是紧的(tight),意味着凸优化求出的解就是原混合整数问题的最优解!这避免了暴力枚举所有可能的离散组合,计算效率大大提升。
但是,这只是单辆车的情况。当多辆车一起博弈时,每辆车的“安全乐高积木块”(顶点)是依赖于其他车的轨迹的!其他车开到哪里,决定了当前车面前有哪些“安全间隙”。这就引出了本文的核心方法:IBR-GCS。IBR-GCS:如何一步步算出“最优反应”?
IBR-GCS,全称基于凸集图的迭代最优响应(Iterative Best Response Graphs of Convex Sets)。它的核心思想是一种“轮流发言,逐步达成共识”的博弈求解方式。
首先,所有车辆有一个初始的、可行的策略(轨迹)。这个初始策略可以很简单,比如大家都保持当前车道和速度。
然后,开始多轮迭代。在每一轮中,车辆依次更新自己的策略。
轮到车i更新时,它会把其他所有车当前最新的策略(轨迹)“冻结”住。基于这些固定不变的轨迹,车i来构建只属于它自己的GCS图。这个图是怎么来的呢?
顶点生成:对于未来每一个时刻t,每一条车道ℓ,车i都会计算其他车辆在该车道造成的“不安全区间”(以其他车辆为中心,前后各一个安全距离dᵢˢ)。那么道路空间减去这些不安全区间,剩下的就是一系列离散的“安全间隙”(safe gap)。每一个(时间t,车道ℓ,安全间隙g)就对应GCS图中的一个顶点,顶点内的连续变量(位置、速度)被约束在这个安全间隙和速度范围内。这就是“策略依赖”的关键体现——其他车的策略决定了车i有哪些顶点可选。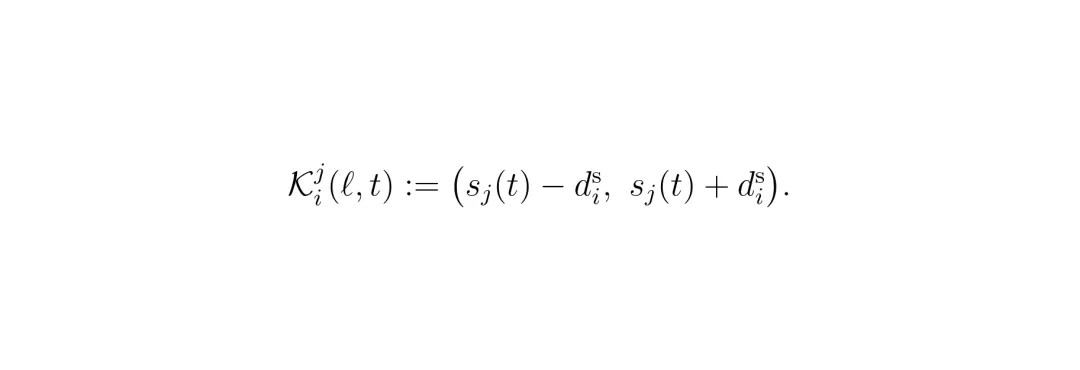 边生成:然后,连接相邻时刻的顶点,形成边。边要满足车辆动力学(位置、速度的递推关系)、加速度限制,以及车道变换逻辑(只能变到相邻车道)。同时,还要考虑横向安全规则(Rule 2):如果两辆车在相邻车道并排行驶(纵向距离很接近),那么禁止它们同时交换车道(防止“对穿”碰撞)。
求解最优路径:建好图之后,车i就面对一个标准的GCS最短路径问题:在考虑自身偏好(跟踪期望速度vᵢᵈᵉˢ、期望车道ℓᵢᵈᵉˢ,最小化加速度和频繁变道)的前提下,找到从起点到终点的成本最低路径。通过求解其凸松弛,车i就得到了针对其他车当前策略的“最优反应”(Best Response)轨迹,并更新自己的策略。(边的成本函数示例,包含速度跟踪、车道偏好、加速度和变道惩罚)
一辆车更新完,下一辆车立即基于最新的全局策略(包括刚更新完的那辆车)来构建自己的GCS图并计算最优反应。如此循环,直到所有车辆都更新一次,完成一轮迭代。
这个过程会反复进行。可以直观地理解:一开始大家的策略可能比较“自私”或“冲突”,但通过轮流计算最优反应,每辆车都在不断适应其他车的新动作,最终整个系统会趋向于一个稳定的、谁单方面改变都不会受益的状态——也就是广义纳什均衡的近似解。
边生成:然后,连接相邻时刻的顶点,形成边。边要满足车辆动力学(位置、速度的递推关系)、加速度限制,以及车道变换逻辑(只能变到相邻车道)。同时,还要考虑横向安全规则(Rule 2):如果两辆车在相邻车道并排行驶(纵向距离很接近),那么禁止它们同时交换车道(防止“对穿”碰撞)。
求解最优路径:建好图之后,车i就面对一个标准的GCS最短路径问题:在考虑自身偏好(跟踪期望速度vᵢᵈᵉˢ、期望车道ℓᵢᵈᵉˢ,最小化加速度和频繁变道)的前提下,找到从起点到终点的成本最低路径。通过求解其凸松弛,车i就得到了针对其他车当前策略的“最优反应”(Best Response)轨迹,并更新自己的策略。(边的成本函数示例,包含速度跟踪、车道偏好、加速度和变道惩罚)
一辆车更新完,下一辆车立即基于最新的全局策略(包括刚更新完的那辆车)来构建自己的GCS图并计算最优反应。如此循环,直到所有车辆都更新一次,完成一轮迭代。
这个过程会反复进行。可以直观地理解:一开始大家的策略可能比较“自私”或“冲突”,但通过轮流计算最优反应,每辆车都在不断适应其他车的新动作,最终整个系统会趋向于一个稳定的、谁单方面改变都不会受益的状态——也就是广义纳什均衡的近似解。理论保证:算法真的能收敛到安全均衡吗?
光有直观描述可不行,数学家们需要严密的证明。本文的一个重要贡献,就是从理论上分析了IBR-GCS的收敛性。
关键在于,本文建模的多车驾驶博弈,在满足以下条件时,是一个广义势博弈(Generalized Potential Game):
1. 车辆目标可分离:每辆车的成本函数只取决于自己的状态和操控,不直接包含对其他车的惩罚或奖励(例如“我讨厌旁边的车”这种主观情绪)。交互只通过共享的安全约束发生。
2. 存在一个全局势函数:这个势函数很简单,就是所有车辆个人成本的总和 Φ(θ) = Σ Jᵢ(θᵢ)。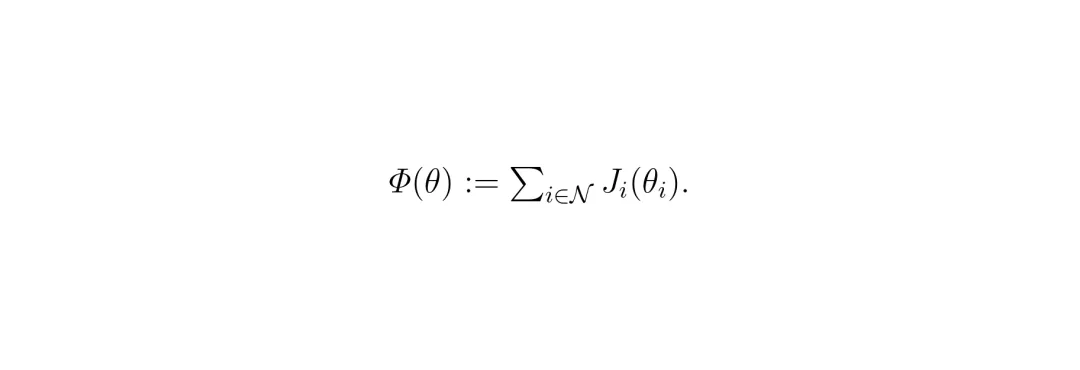 在广义势博弈中,有一个美妙性质:任何一辆车单方面做出一个能降低自己成本的“最优反应”时,全局势函数的值也一定会下降(或至少不增加)。
在广义势博弈中,有一个美妙性质:任何一辆车单方面做出一个能降低自己成本的“最优反应”时,全局势函数的值也一定会下降(或至少不增加)。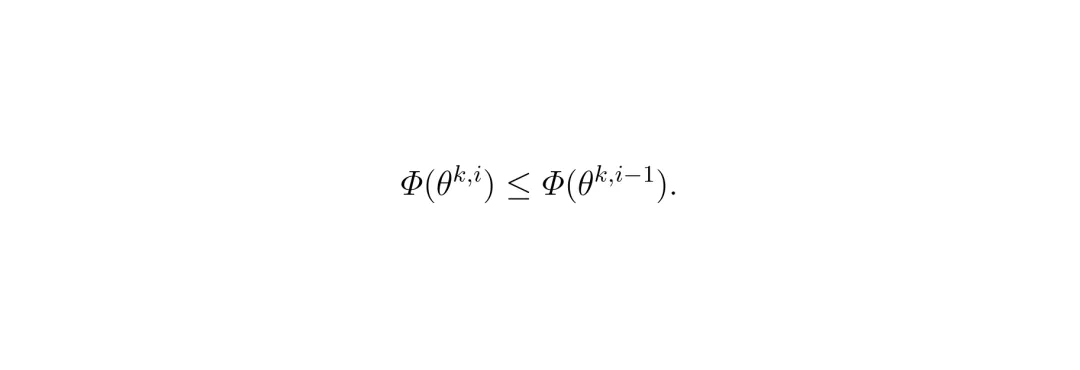 因此,如果每次迭代中每辆车都能计算出精确的最优反应,那么IBR过程就会让势函数值单调递减。由于势函数有下界(成本非负),算法最终会收敛。
但现实中,我们求解GCS最短路径用的是凸松弛,如果松弛不紧,得到的就是一个近似最优反应。本文进一步分析了这种近似性带来的影响。论文证明,如果每个近似最优反应的误差(相比真正的最优解)有一个一致的上界ε̄,那么IBR-GCS迭代生成的策略序列,其最大后悔值(任何一辆车单方面还能改进的幅度)在极限情况下也不会超过ε̄。也就是说,算法会收敛到一个ε̄-广义纳什均衡的邻域内。
因此,如果每次迭代中每辆车都能计算出精确的最优反应,那么IBR过程就会让势函数值单调递减。由于势函数有下界(成本非负),算法最终会收敛。
但现实中,我们求解GCS最短路径用的是凸松弛,如果松弛不紧,得到的就是一个近似最优反应。本文进一步分析了这种近似性带来的影响。论文证明,如果每个近似最优反应的误差(相比真正的最优解)有一个一致的上界ε̄,那么IBR-GCS迭代生成的策略序列,其最大后悔值(任何一辆车单方面还能改进的幅度)在极限情况下也不会超过ε̄。也就是说,算法会收敛到一个ε̄-广义纳什均衡的邻域内。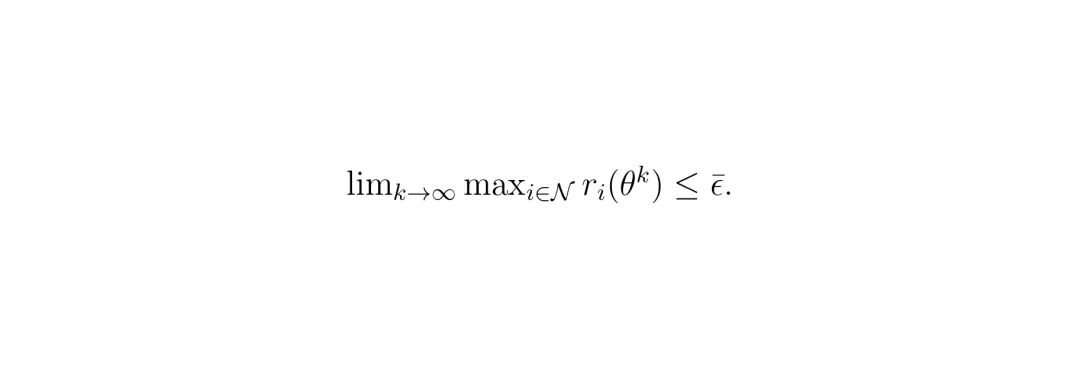 这就为算法的实际应用提供了理论上的安心丸。当然,作者也坦率指出,GCS凸松弛的紧致性在理论上难以保证(虽然实践中常常很紧),所以这个“一致误差上界”的假设是需要留意的。
这就为算法的实际应用提供了理论上的安心丸。当然,作者也坦率指出,GCS凸松弛的紧致性在理论上难以保证(虽然实践中常常很紧),所以这个“一致误差上界”的假设是需要留意的。仿真验证:复杂合并场景下的智能博弈
理论再漂亮,也得拉出来遛遛。论文在一个经典的复杂场景中验证了IBR-GCS:两条车道合并到一条三车道高速公路,总共6辆车参与博弈。图4:六辆车在有一条合并车道的高速公路上的轨迹。每辆车的初始和最终位置以不透明显示,而每三个时间步的位置以半透明显示。
从图4的轨迹图可以看到,算法生成的策略非常智能且符合人类直觉:
安全避让:所有车辆在整个规划时域内都保持了安全的纵向和横向距离,没有碰撞风险。
协同博弈:车辆之间表现出了协同行为。例如,为了给合并车辆让出空间,已有车道上的车辆可能会适度减速或变换车道,而合并车辆也会选择恰当的时机和间隙切入。
目标达成:车辆在保证安全的同时,也尽可能地跟踪了自己的期望速度和期望车道。
整个算法仅用了2轮迭代就收敛了,总计算时间(在消费级笔记本CPU上)约为297秒。虽然离实时(秒级)还有距离,但对于离线规划或低频率重规划来说,已经展示了其处理复杂交互场景的潜力。
为了更全面地评估,论文还进行了100次随机化参数的仿真(4辆车,3车道)。结果如图5所示,势函数值随着迭代进行严格单调下降,这强有力地验证了之前理论分析的正确性,也表明GCS凸松弛在实践中确实非常紧致。图5:100次随机仿真设置中势函数随迭代次数演化的分布,橙色曲线为均值。如图所示,势函数在第k次迭代时总是小于第k-1次迭代。局限与展望:从理论到实车的距离还有多远?
IBR-GCS无疑为多车博弈规划提供了一个兼具理论美感与实用潜力的框架。但论文作者也清醒地指出了当前的局限和未来方向:
1. 计算效率:虽然比传统混合整数规划快,但目前的实现(每轮迭代每辆车都重建整个GCS图)离实时车载计算还有差距。未来可以通过增量更新图结构、利用上一次求解的结果进行热启动等工程优化来大幅提速。
2. 均衡的选择与更新顺序:IBR算法最终收敛到的均衡点,可能依赖于初始策略和车辆更新的顺序。这在博弈论中是常见现象。如何设计更鲁棒或更公平的更新机制(例如随机顺序、基于优先级的顺序)值得探索。
3. 模型简化:本文使用了相对简化的车辆动力学和道路模型(笔直车道)。扩展到弯曲道路、更复杂的车辆模型(如自行车模型),以及包含不确定性(感知、预测误差)的不完全信息博弈,是迈向实际应用的关键一步。
4. 理论紧致性:尽管实验表现良好,但GCS凸松弛的紧致性在理论上仍缺乏一般性保证。为自动驾驶这类特定问题寻找并证明其紧致条件,将是非常有价值的理论工作。龙迷三问
这篇论文解决的核心问题是什么?它解决的是多辆自动驾驶车辆在共享道路(如高速公路)上,如何进行安全、高效且具有策略性交互的轨迹规划问题。传统方法要么忽略其他车的策略意图,要么计算过于复杂。本文用博弈论建模交互,用凸集图(GCS)高效处理混合整数规划,提出了IBR-GCS算法,旨在找到车辆们的一个均衡策略,使得没有车愿意单方面违反规则或损害自身利益去改变路线。
GCS(凸集图)和传统的图搜索(如A*)有什么区别?核心区别在于顶点和边的内涵。传统图搜索的顶点通常是一个离散的“状态点”(如网格坐标),边代表点与点之间的连接。而GCS的顶点是一个连续的凸集区域(比如一段安全的位置区间),边代表两个区域之间动态可行的转移,并带有连续的优化成本。因此,GCS在搜索离散路径的同时,内嵌了连续空间的轨迹优化,并且其凸松弛形式可以高效求解,避免了在连续空间中采样或离散化过粗的问题。
“广义纳什均衡”在自动驾驶中意味着什么?对我们乘客有什么好处?在本文的上下文中,达到广义纳什均衡意味着生成了一套协同的、可预测的、稳定的多车行驶方案。好处包括:安全性:均衡策略天然满足所有安全约束。效率与舒适性:车辆间通过博弈达成“默契”,减少急刹、僵持等低效或令人不适的交互。可预测性:所有AI车辆都按这个均衡策略行驶,彼此的行为更可预测,从而提升整体交通流的平滑度。
如果你还有哪些想要了解的,欢迎在评论区留言或者讨论~龙哥点评
论文创新性分数:★★★★☆
将前沿的GCS框架与非合作博弈论结合,用于解决多车交互规划这一具体且重要的问题,构思巧妙。核心创新点“策略依赖的GCS构建”和“在广义势博弈框架下的IBR求解”具有很好的原创性。实验合理度:★★★★☆
实验设计聚焦于验证核心主张:方法能处理复杂交互、生成安全轨迹、并收敛到近似均衡。定量的势函数下降曲线和定性的轨迹可视化提供了有力证据。但主要与基线方法的定量对比稍显不足。学术研究价值:★★★★★
价值很高。为“博弈论+凸优化”解决混合整数交互规划问题提供了一个清晰、可扩展的模板。理论部分对近似IBR收敛性的分析严谨,对后续研究有指导意义。开源代码基于成熟的GCSOPT库,复现和借鉴门槛降低。稳定性:★★★☆☆
在仿真的确定性环境下表现出色。但方法严重依赖于GCS凸松弛的紧致性,虽然文中实验显示很紧,但理论上存在不紧的可能,这会影响最优反应计算的准确性,从而影响整个IBR过程的稳定性。对于感知不确定性也未做考虑。适应性以及泛化能力:★★★☆☆
目前框架针对笔直车道、简化动力学和完全信息博弈设计。要适应弯曲道路、复杂路口、更精细的车辆模型以及不完全信息场景,需要大量的框架扩展和工程工作,非直接迁移。硬件需求及成本:★★☆☆☆
计算成本较高。每轮迭代每辆车需求解一个中等规模的凸优化问题(GCS最短路径松弛),6辆车场景迭代2轮总耗时近300秒(笔记本CPU)。离实时车载计算要求差距显著,更适用于离线仿真或作为上层决策器。复现难度:★★★★☆
难度中等。论文依赖的GCSOPT库已开源,核心算法流程描述清晰。但构建完整的仿真环境和实现所有约束细节仍需一定工程能力。对于不熟悉凸优化和博弈论的读者,理论部分理解有门槛。产品化成熟度:★☆☆☆☆
目前仅为研究原型阶段。计算速度、对不确定性的处理、复杂场景的泛化能力均未达到产品级要求。其主要价值在于指明了技术方向,并提供了理论基础和算法框架。可能的问题:本文是一项出色的“框架性”研究,但如同许多论文,在追求方法优雅和理论深度的同时,对计算复杂度的现实约束、与现有SOTA方法的全面性能对比、以及向嘈杂现实世界推广的鲁棒性探讨尚显不足。这为后续的工程化研究留下了明确空间。
[1] Marcucci, T., Umenberger, J., Parrilo, P., & Tedrake, R. (2024). Shortest Paths in Graphs of Convex Sets. SIAM Journal on Optimization. (GCS基础理论)[2] Monderer, D., & Shapley, L. S. (1996). Potential Games. Games and Economic Behavior. (势博弈理论基础)[3] Wang, M., et al. (2021). Game-Theoretic Planning for Self-Driving Cars in Multivehicle Competitive Scenarios. IEEE Transactions on Robotics. (自动驾驶博弈规划相关工作)[4] 本文原文:Käfer, N., Khalil, A., Huynh, E., Bakolas, E., & Fridovich-Keil, D. (2026). Game-Theoretic Autonomous Driving: A Graphs of Convex Sets Approach. arXiv:2601.20054.*本文仅代表个人理解及观点,不构成任何论文审核或者项目落地推荐意见,具体以相关组织评审结果为准。欢迎就论文内容交流探讨,理性发言哦~ 想了解更多原文细节的小伙伴,可以点击左下角的"阅读原文",查看更多原论文细节哦!

🚗 还在为多车博弈的复杂规划头秃吗?想和同行大佬一起探讨自动驾驶前沿算法?
欢迎加入龙哥读论文粉丝群,
扫描下方二维码或者添加龙哥助手微信号加群:kangjinlonghelper。
一定要备注:研究方向+地点+学校/公司+昵称(如 自动驾驶+北京+清华+龙哥),根据格式备注,可更快被通过且邀请进群。

