自动驾驶雷达干扰缓解：探索主动策略论文精读

C. Aydogdu et al., "Radar Interference Mitigation for Automated Driving: Exploring Proactive Strategies," in IEEE Signal Processing Magazine, vol. 37, no. 4, pp. 72-84, July 2020, doi: 10.1109/MSP.2020.2969319.

这篇文章的主线很清晰：车载FMCW雷达在密集交通环境中会互相“照射”，而且这种干扰往往远强于目标回波；传统“事后补救”的抗干扰方法在车联网高度动态场景里可能不够用，于是作者系统分析了干扰机理与概率，并提出三类更偏“事前设计/协同”的主动策略：准正交FMCW波形、基于低速通信的资源协调、以及RadCom/OFDM体制。

1. 问题图景：为什么车载雷达干扰会变成“硬问题”

文章开头强调一个现实趋势：ADAS/自动驾驶普及带来路网中雷达收发机数量激增，且大多无协同地发射，干扰事件将显著增加。作者明确本文聚焦FMCW（最常见、最鲁棒的车载雷达），并将干扰影响量化为概率、严重度、以及对检测/跟踪的具体后果（虚警、漏检、鬼影目标等）。

下面这张图给出了“互相照射”场景：多车同频段雷达工作，某车的回波链路是“两程”衰落，而别车的直达干扰是“一程”传播，天然就更强。

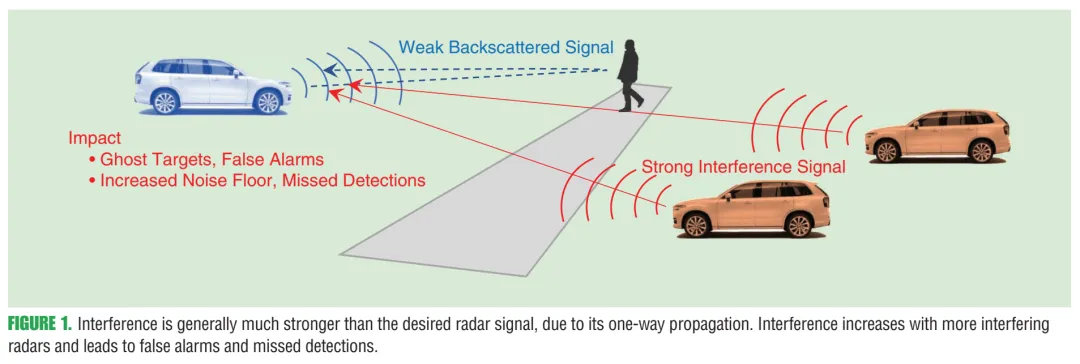
图1内容：多车雷达同时工作导致互扰；干扰路径多为雷达到雷达的直达链路（单程），而目标回波是雷达→目标→雷达（双程）。原文图注强调这是“radar interference problem illustration”。

2. FMCW体制与信号处理链：从发射到“距离-速度图”

文章用标准的K个线性调频chirp（sweep）描述FMCW发射信号。一个帧内K个chirp连续发射（此处作者假设无chirp间空闲，但也指出引入随机空闲可降低互扰概率）。

2.1 发射信号模型（式(1)(2)）

帧信号写成

其中单个chirp

这里  为扫频带宽、 为chirp时长、 为载频、 为chirp斜率。

2.2 回波模型与“停-走假设”（式(3)）

假设单个点目标，复信道增益 （包含路径损耗、天线增益、RCS等）、往返传播时延

归一化多普勒

则在 stop-and-hop 假设下第  个chirp的接收信号形式为

其中  是相对chirp起点的快时间， 为噪声。

2.3 图2：典型FMCW雷达收发链与处理流程（带“干扰插入点”）

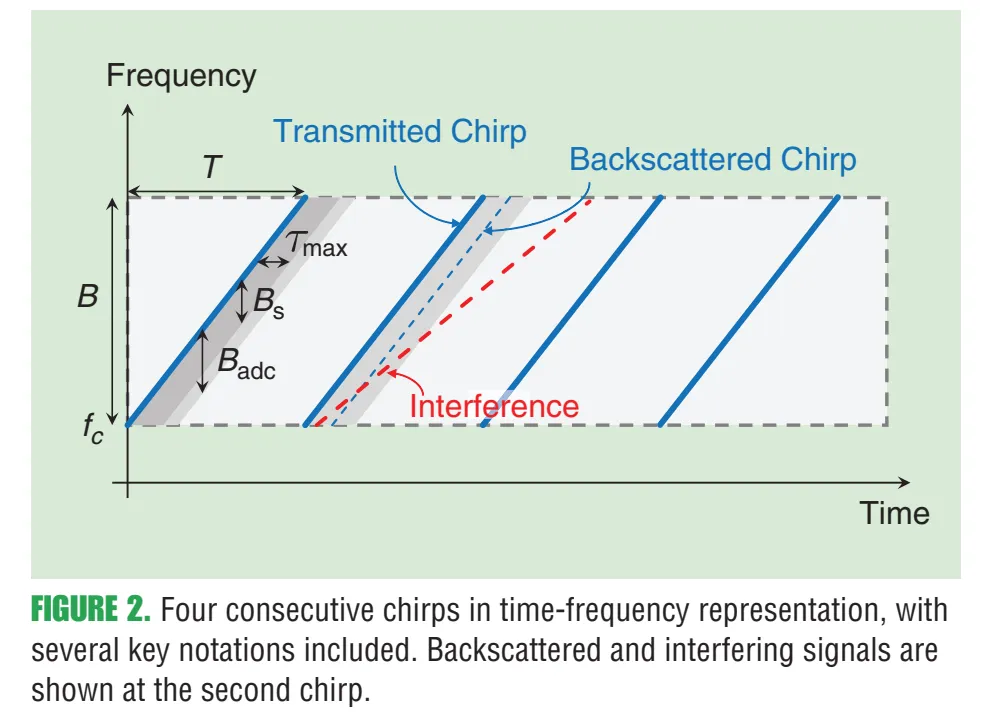
图2内容：从Tx基带→RF前端→接收端低噪放→混频“去chirp”(dechirp)→低通滤波→ADC→FFT/二维处理→检测/跟踪。图中还明确了干扰可能在混频后以“拍频/伪峰/噪底抬升”的方式进入后续处理链。原文图注为“FMCW radar signal processing chain”。

2.4 Stage 1：Dechirping 得到拍频信号（式(4)(5)）

接收信号与本振（本机发射）做共轭混频（dechirp），并忽略在一个CPI内相位总进动很小的项后，作者给出拍频（中频）信号近似为

并对快时间采样  得到

这两式揭示：拍频里“距离项 ”与“多普勒项 ”发生耦合（），后面做二维匹配滤波/FFT时要处理这种range–Doppler coupling。

3. Delay–Doppler谱：二维匹配滤波（式(6)）与分辨率

Stage 2中，作者把  做二维指数匹配（可视作二维DFT/periodogram），定义某个时延-多普勒点  上的delay–Doppler响应为

该谱在真实目标附近产生峰值，常配合CFAR做检测；峰值与处理增益  成正比。作者也指出其中的  是由FMCW固有的耦合引起的时延偏移，可在估计后补偿。

更关键的是，作者直接从式(6)给出FMCW的距离与速度分辨率（在  足够大时）

其中  为载波波长。直观解释：带宽越大→距离分辨率越高；CPI越长（ 越大）→速度分辨率越高。

4. 干扰为何“天然更强”：Friis vs Radar Equation（式(7)）

单链路下，作者用一个对比说明“为啥这事麻烦”： 目标回波受雷达方程（双程） 支配；而他车直达干扰受 Friis自由空间传播（单程） 支配，于是干扰功率远大于回波功率。

文中给出（符号按原文）回波与干扰功率的关系式（式(7)），核心结构是

因此在  与  同量级且 （RCS）取常见值时，通常 。

这也解释了后文为何把干扰影响拆成两部分：一是“强度”（功率），二是“相干性”（是否会像目标一样形成尖锐峰/鬼影）。

5. 频谱现象：chirp斜率失配、相位噪声与“鬼影/噪底抬升”

5.1 图3：chirp斜率失配导致干扰能量在距离谱里“铺开/挤压”

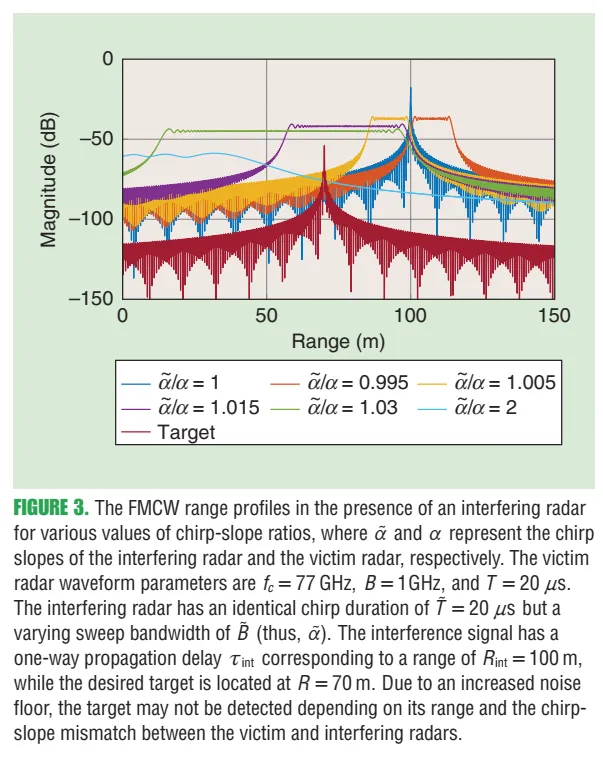
图3内容：受害雷达的距离谱在存在干扰雷达时，随斜率比  改变而出现明显差异：当斜率匹配程度不同，干扰在距离轴上的“形态”不同，可能形成局部峰值、也可能把噪底整体抬高，从而掩盖弱目标或引入虚假峰。原文说明参数如 GHz、GHz、 等，并强调干扰是单程传播而目标是双程传播。

5.2 图4：相位噪声造成谱展宽，细节丢失，弱目标更易被掩盖

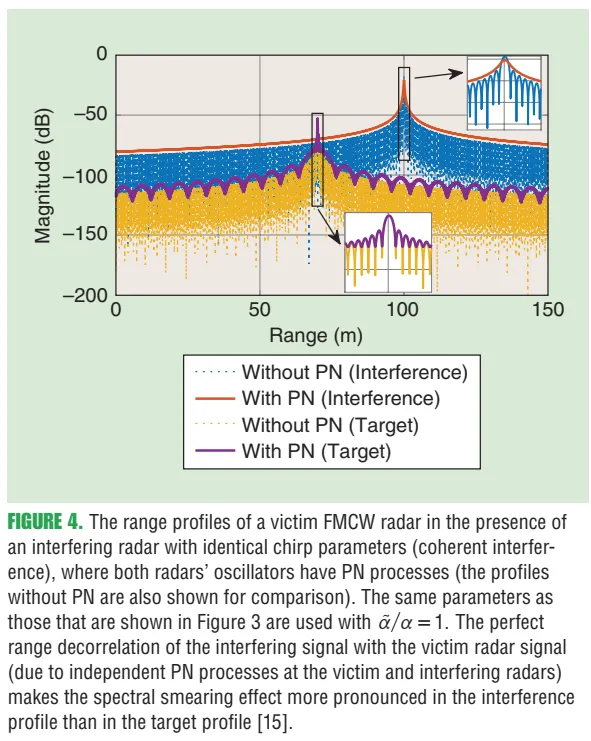
图4内容：考虑振荡器相位噪声（PN）后，无论目标回波还是干扰谱都会“涂抹/展宽”，但由于干扰更强，这种谱展宽会更显著地恶化检测性能，尤其会遮蔽弱目标。原文图注指出这里讨论“相干干扰”场景，并对比“有/无PN”两种情况。

6. 从单车到路网：随机几何下的网络干扰（图5、式(8)(9)）

作者把道路上车辆位置抽象为随机点过程，用随机几何分析平均干扰。关键设定是：在多车道高速路上，每条车道的车辆（或雷达）沿道路方向形成一维Poisson点过程 ，强度 （ 是平均车距）。

图5：六车道高速路的网络干扰示意

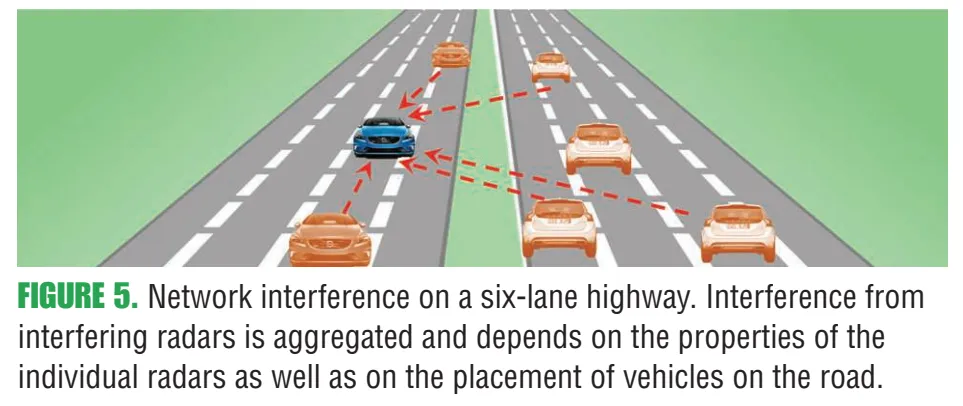
图5内容解读：受害车位于某条车道，周围多车道（对向、同向超车道等）车辆均可能形成干扰；作者将来自不同车道的干扰叠加，强调它与车辆空间分布、天线视场(FOV)等密切相关。

6.1 车道  的聚合干扰（式(8)）

作者将某条车道  上所有干扰车的贡献累加，写成（结构上是“点过程求和”）

其中  是从受害车到位置  的干扰车的距离， 是“发生干扰的概率/占空相关因子”（后面会精确解释），并且天线/FOV通过积分下限或增益项进入。

6.2 期望干扰（式(9)）的连续化积分形式

对Poisson点过程用平均化（本质上是Campbell定理），作者把干扰期望写成积分形式，并得到与 （平均车距）成反比的趋势项。文中给出一个代表性化简结果（展示“车越密→干扰越大”的量化规律）：

这里  是车道间距， 与FOV有关，积分下限体现“视场外不计入干扰”。

7. 图6：网络干扰如何抬升噪底并压垮SINR

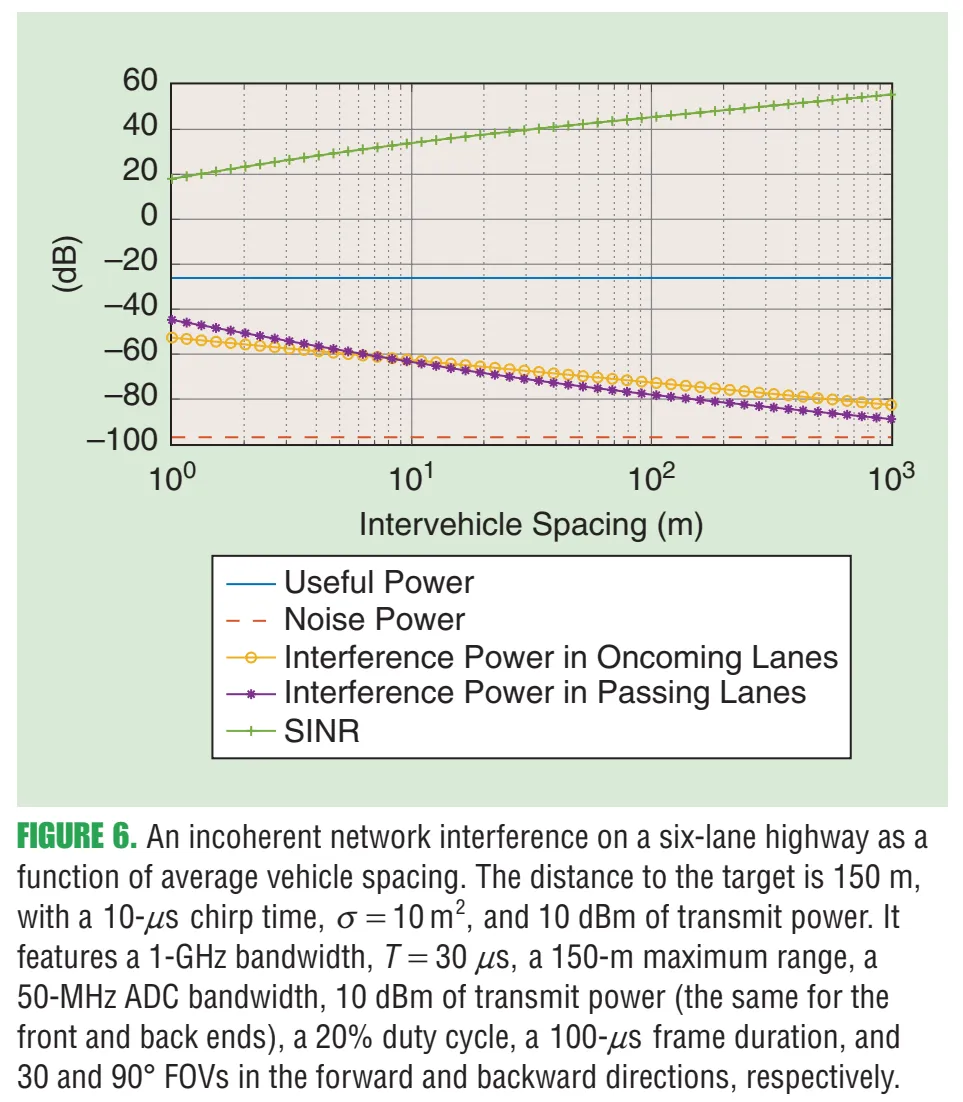
图6内容：横轴是平均车距（越小表示越拥挤），纵轴展示 useful power、noise power、来自对向车道/超车车道的干扰功率，以及合成后的SINR。随着车距减小，干扰项迅速上升，SINR大幅下降；作者还给出实验/仿真设定，例如目标距离150 m、带宽1 GHz、占空20%、不同FOV等。

这张图把“网络层面”的结论说得很直白：即便是非相干干扰，也能把噪底抬升“几十dB”量级，从而让弱目标（行人/自行车等低RCS）更难检测。

8. 把影响压成一个“可设计的指标”：SIR表达式（式(10)(11)）

作者用一种工程上非常好用的方式，把目标峰值（有用）与干扰功率写成

其中  描述干扰与处理增益的耦合（相干程度不同， 取值区间不同）。

进而得到SIR（式(11)）的分解形式：

（原文把“不可控因素”和“可控因素”分开强调：第一因子多由场景决定，第二因子可通过占空比、chirp斜率、FOV、处理增益等优化，使SIR远大于1。）

这里已经埋下后文三种主动策略的逻辑：降低  、降低有效斜率  或通过资源分离让“相干叠加”变得不可能，同时保持足够的距离/速度分辨率。

9. 主动策略一：准正交FMCW波形（图7、式(12)及其后推导）

作者从前面的分析得到一个干净的比例关系：干扰与

相关（ 为占空比， 为最大往返时延），因此 降低chirp斜率  （等价于延长chirp）能显著降低干扰。

9.1 两个错位chirp的耦合（式(12)）

考虑一个chirp  与时间错位  的chirp （并以周期  重复），它们的功率泄漏/耦合（本质上是相关积分）：

并指出由于瞬时频差约为 ，所以这种耦合像“两正弦频差”的互相关一样迅速衰减，从而称这些波形为准正交。

9.2 图7：单慢扫频(slow-sweep) FMCW实现“很多近似正交信号”

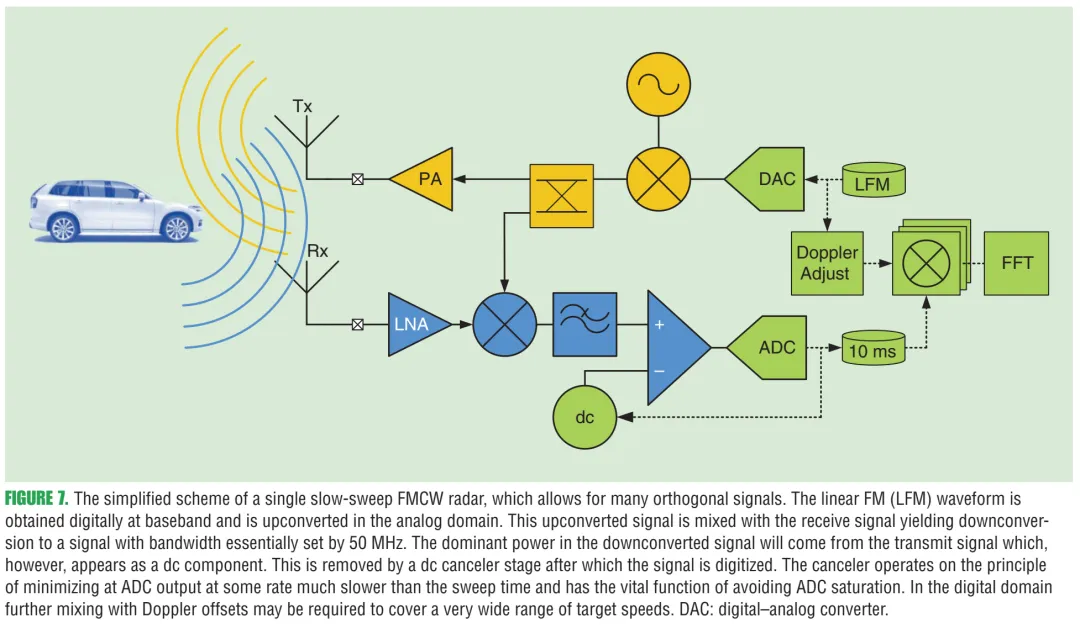
图7内容：这是一个“把慢扫频FMCW落地到硬件链路”的简化方案。LFM基带可数字生成，上变频后发射；接收端下变频得到基带后以约50 MHz带宽采样；强泄漏在数字域表现为直流分量，通过“dc消除/反馈抵消”而非极低截止频率的模拟高通来处理；同时允许在数字域做相位偏置（Doppler adjust）以改变不模糊速度范围。原文图注强调该方案“允许许多正交信号”，并解释了DAC/ADC/直流消除等关键模块。

9.3 “长chirp”下的速度-距离解耦（式(13)(14)的意义）

作者指出式(5)里把速度当作简单多普勒近似会忽略小项，但在长chirp下必须保留，从而可在单chirp内解决range-speed ambiguity。文中写出更严格的形式（结构上是“相位含二次项的积分”）并用频域峰值与相位单调性做数值反演来求速度。

10. 主动策略二：借助低速通信做“频时资源协调”（图8、图9）

这部分作者把雷达当作“可被调度的发射机”，通过低速通信在车与车之间交换起始时间/频带等信息，使雷达在频时资源上尽量正交。文章提到可以用专用通信或蜂窝V2X，甚至把雷达与通信融合成RadCom单元。

10.1 图8：RCU的频时共享与冲突消解机制

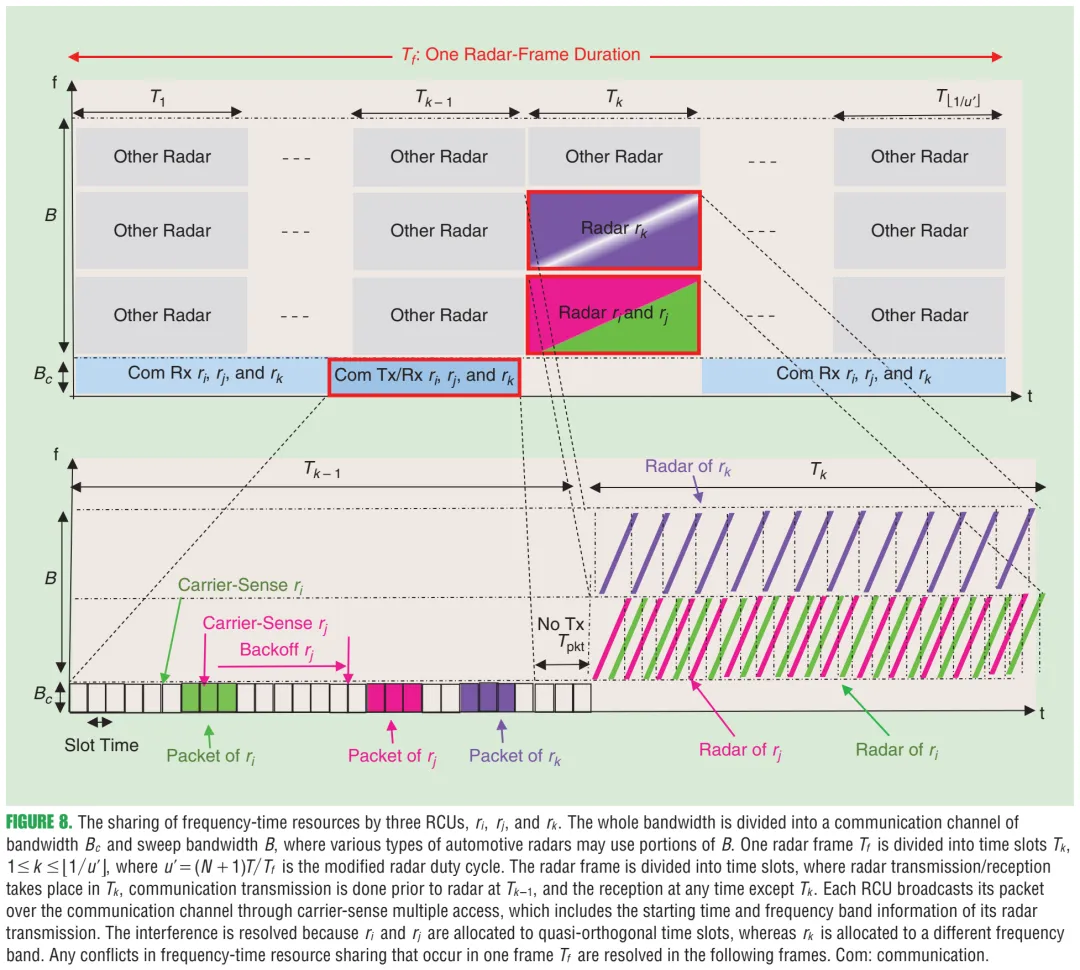
图8内容解读：上半部分展示一个雷达帧  被切成时间槽，车载RCU在通信带宽  上广播自己的“雷达资源占用”，从而把不同车辆的雷达chirp安排到准正交的时间槽；若某车被分配到不同频带，则通过频分避免冲突。下半部分展示载波侦听/退避的通信过程与“下一帧再消解冲突”的思想。原文图注还解释了  三个RCU：前两者用准正交时间槽，第三者换频带，且帧内冲突可在后续帧消解。

10.2 图9：协调前后干扰概率  的数量级差异

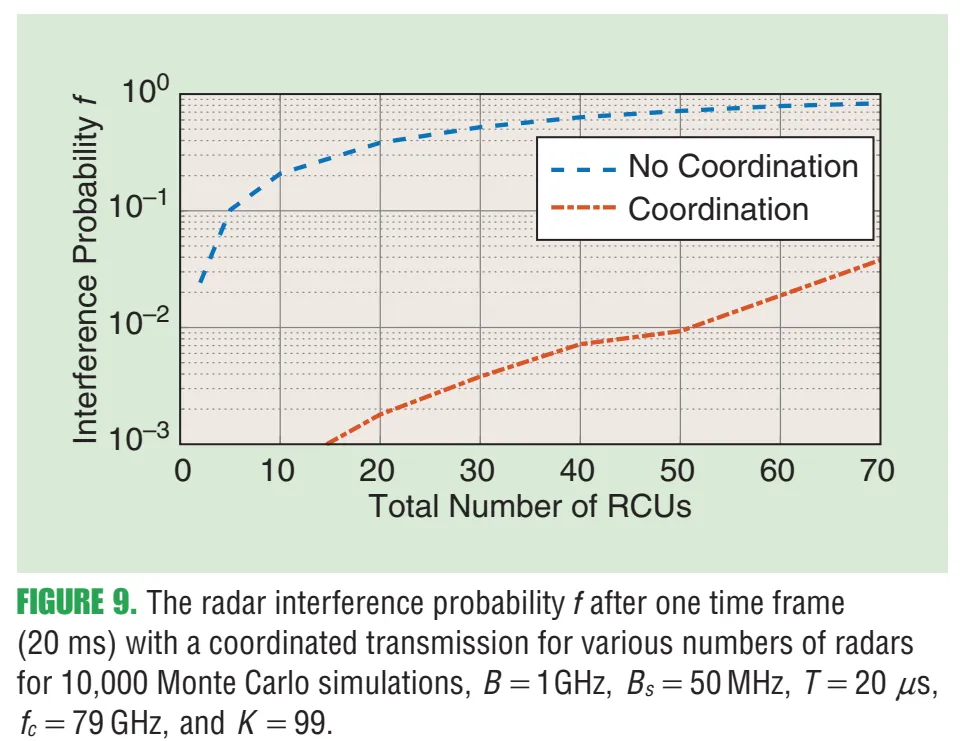
图9内容解读：横轴为RCU（雷达/通信单元）数量，纵轴为干扰概率 （对Monte Carlo取期望意义）。图中“Coordination”曲线显著低于“No Coordination”，说明只要能在几十毫秒级做资源分配更新，干扰概率能大幅降低。原文图注给出仿真条件：一个帧20 ms、1 GHz带宽、 MHz、 ns、 GHz、、10,000次Monte Carlo等。

11. 主动策略三：RadCom / OFDM，尤其是“跳频的 stepped-frequency OFDM”（图10、式(15)、图11）

作者指出OFDM作为通信主力波形，天然适合做“雷达+通信”融合（RadCom）。难点在于常规OFDM雷达受ADC带宽限制，分辨率不如宽带FMCW；解决思路是用stepped-frequency OFDM：连续OFDM帧在不同载频上发射，拼接成更大的总带宽，同时每帧仍保持较小的基带带宽，从而降低ADC速率。

11.1 图10：时间-频率资源协调示意（stepped vs narrow-band）

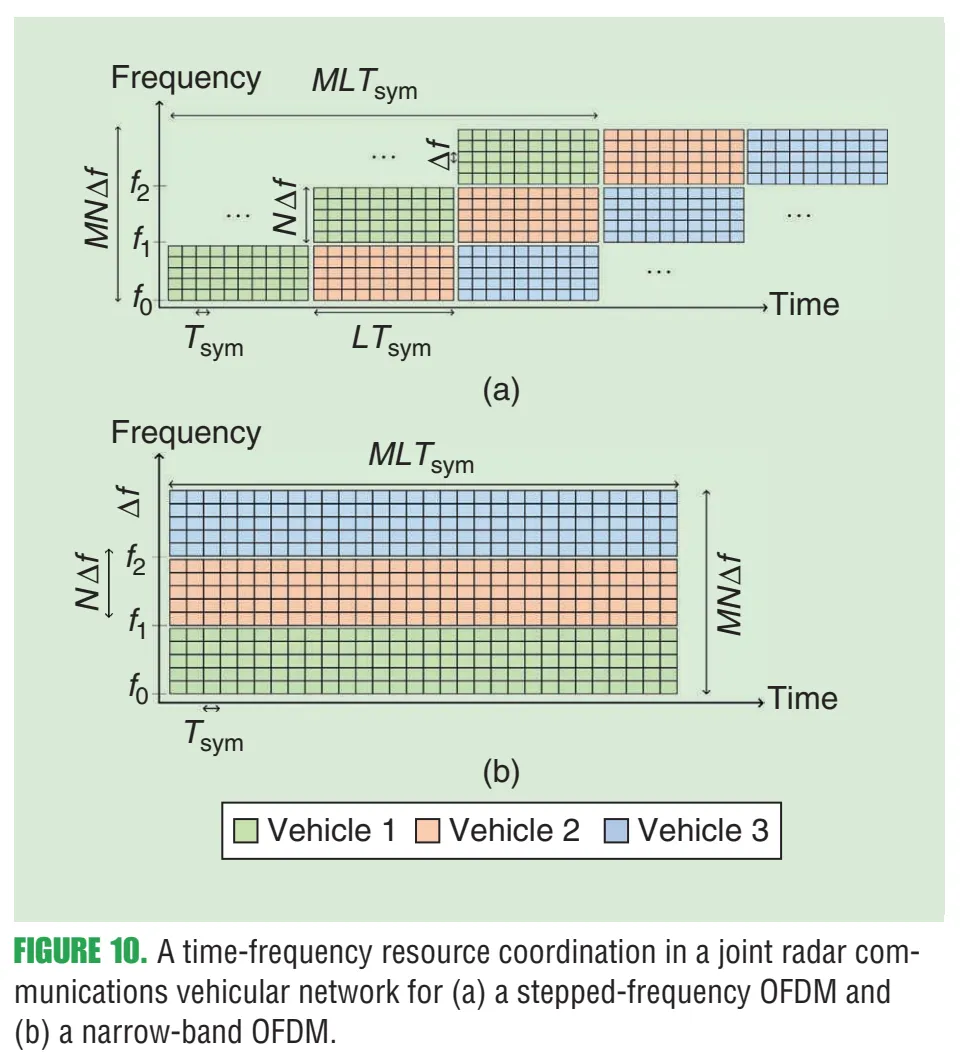
图10内容解读：图10(a)显示stepped-frequency OFDM：不同车辆被分配到互不重叠的时频块（不同载频/不同时间段），每个车辆通过跨M个载频帧的联合处理获得总带宽  的高距离分辨率；图10(b)为窄带OFDM的资源分配。原文图注明确这是“time-frequency resource coordination in a joint radar communications vehicular network”。

11.2 OFDM回波数据立方体模型（式(15)）

在“循环前缀长于时延、且小多普勒近似”等标准假设下，作者给出第  帧、第  个符号、第  个子载波上的接收符号模型

其中  是发射数据/导频符号， 为噪声。作者随后说明：对  维做匹配滤波可估计时延，对  维处理可估计多普勒；跳频带来delay–Doppler耦合，可通过DFT实现里的相位校正项消除。

11.3 图11：三种OFDM方案下“可容纳车辆数”的对比

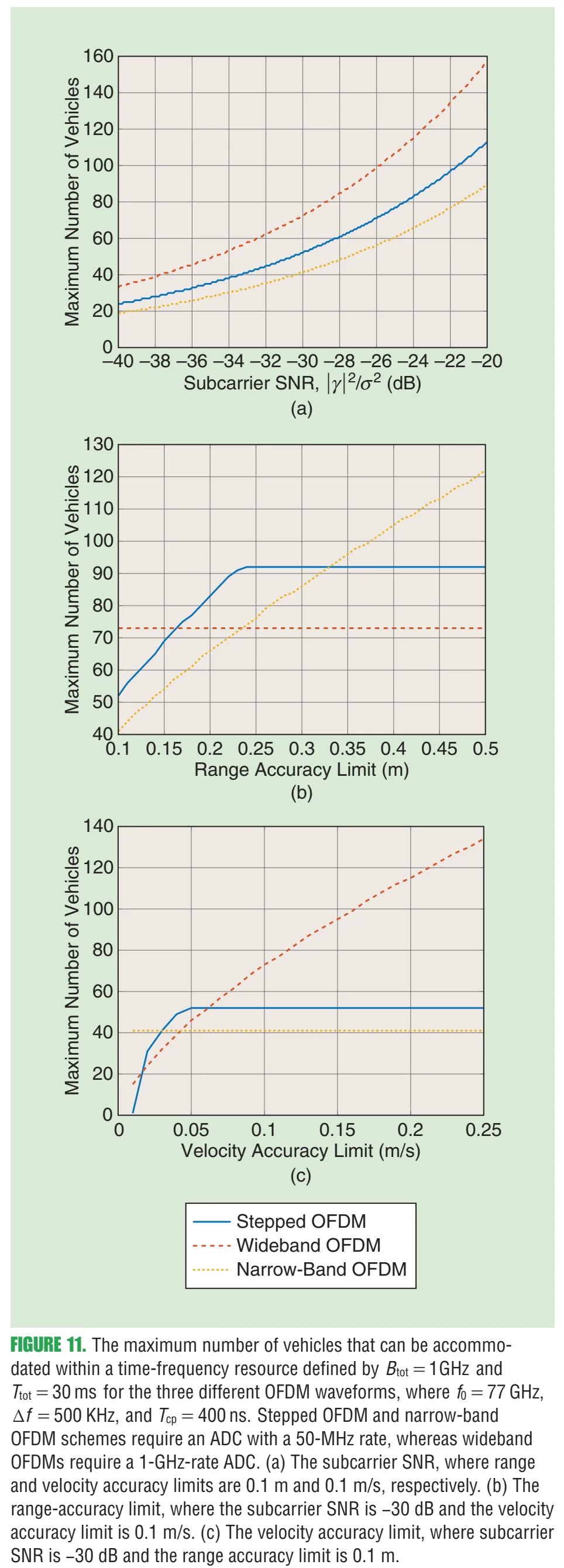
图11内容：给定总资源  GHz 与  ms，比较 stepped-frequency、窄带、宽带OFDM三种方案可支持的车辆数；stepped-frequency在相同ADC（50 MHz）硬件约束下，通过“跳频换距离精度、牺牲部分多普勒精度”的灵活权衡，往往能塞进更多车辆。原文图注还说明宽带OFDM需要1 GHz采样率ADC，且(a)(b)(c)分别在不同精度/SNR约束下比较。

12. 图12：验证平台与实验环境

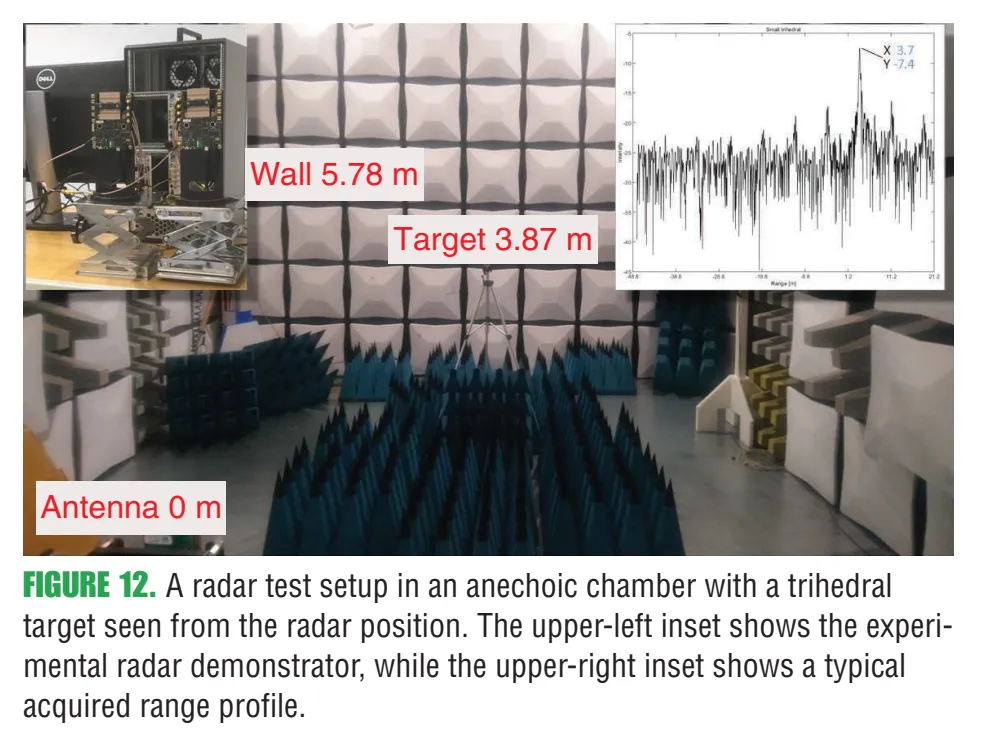
图12内容：作者 计划 搭建包含毫米波前端、高速数字信号生成与采集、以及可控“独立干扰源”的演示平台，并在更真实环境里验证前文关于干扰概率、SINR、以及slow-ramp测速方法的理论分析。图中展示暗室(anechoic chamber)内的壁面与目标位置标注、以及典型距离谱插图。

附录：关键推导

A.1 从chirp模型推到拍频与“距离-速度耦合”（式(4)(5)的展开）

发射chirp：

单目标回波（忽略幅度常数，保留时延与多普勒）可写成

dechirp就是与本机chirp共轭相乘：

把  的相位展开：

把常数相位合并到  中（或写成  的形式），于是

再把  与  合并，就得到原文式(4)的“拍频指数项”结构：

对应采样  直接得

与原文式(4)(5)同型。

这里的关键点是：在单个chirp内，快时间频率项是 ，所以距离与速度混在一起；必须通过跨chirp的慢时间维度（ 维）来把  单独拉出来。

A.2 从二维periodogram推分辨率：为什么 ，

式(6)本质是对二维复指数的匹配滤波/DFT：

把无噪单目标的  代入：

两项都是有限长度几何级数，其幅度包络是Dirichlet核；主瓣零点间隔由指数“频率”的分辨力决定。

• 距离（时延）分辨率来自第二项对  的敏感度。令

  当  已靠近 （或把耦合补偿后），主瓣主要由  决定。第二项主瓣宽度满足

  又因为快时间观测长度 ，且 ，得

  换成距离 ，于是

  即原文给出的 。

• 速度（多普勒）分辨率来自第一项对  的敏感度。其主瓣宽度满足

  将 ，得

  原文写成  的等价形式，是因为在很多雷达教材里用 ，两者只差“用  还是用 ”的记号。

A.3 “干扰概率因子”  的来源：为什么它会与占空比/ADC带宽/斜率相关（通向式(11)）

在FMCW里，干扰并非总是“全时全频”落在受害雷达的有效拍频带内。作者在式(11)前的推导把“会造成有效干扰的时间/频率重叠比例”压成一个概率因子 ，并强调可通过设计减小它。

一个常见推导思路（与文中“干扰与  等成比例”的结论一致）如下：

dechirp后，来自干扰雷达的拍频会出现在受害雷达的低通+ADC带宽  内，条件近似可写成

当车辆位置/起始时间随机时， 在  的有效范围内变化（），而拍频随  的变化率就是斜率 。因此“落入带宽窗”的概率量级

具体系数与精确假设有关，但依赖关系与作者在准正交部分写的

一致（这里  对应最大往返时延）。

这也解释了三种主动策略分别在“降低有效斜率/延长chirp”“降低重叠概率（调度）”“把资源做成严格正交（OFDM时频分配）”三个方向发力。

A.4 从点过程求和到积分期望：式(8)→式(9)的详细一步

式(8)是车道  上Poisson点过程  的求和形式。 为了求其期望，用Campbell定理：

其中 。

把  代入，得到

几何关系：若车道中心线与受害车道相距 ，且把沿道路方向的坐标写成 ，则

同时，由FOV限制（只有进入视场的干扰才算），积分下限从某个 （半视场角）开始。用 （即 ）变换，，并且

于是

将  代回，就得到式(9)那种“与 、、 成简单比例”的结果形态（文中给的是同类化简表达式，并强调小  处需要安全边界避免奇异）。

A.5 从式(10)到式(11)：把“可设计量”显式拆出来

式(10)给出

于是

接下来用“目标回波由雷达方程决定、干扰由Friis决定”的功率比（式(7)）把  替换成与  有关的比例，再把  展开成与占空比 、斜率 、ADC带宽 、以及FOV（通过发生重叠的概率）相关的因子，就得到式(11)那种“第一因子不可控、第二因子可控”的结构。作者在正文里直接强调可控项包括：小占空比、小斜率（或小  比例）、缩小FOV以减小 、以及增大有效处理增益 。